Dividend Value Builder Newsletter
Intrinsic Value and Its Relationship to Margin of Safety
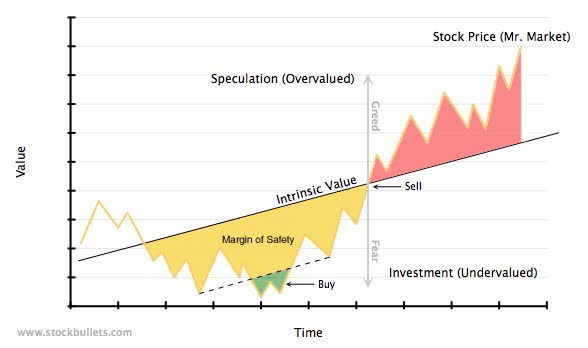
The purpose of this post is to examine intrinsic value and its relationship to margin of safety. The two go hand in hand, or at least they should. These two concepts are the backbone of value investing and the basis for Benjamin Graham’s book, The Intelligent Investor.
Intrinsic value (a.k.a. fundamental value), is the perceived value of an investment’s future cash flow, expected growth, and risk. In other words, intrinsic value is the future cash flow discounted back to a present value.
While the definition may be quite simple the calculation is much harder or imprecise. Because there are literally hundreds of variables that go into the estimate of intrinsic value, the accuracy of such a calculation is dubious at best. We will talk about how to overcome this dilemma shortly.
Additional Reading: Intrinsic Value Stock Analysis – My Formula
Intrinsic Value vs. Market Value
Understand the intrinsic value may be significantly different from the market value or price of the investment. The market price is the price you can buy and sell the asset (i.e a stock quote). Buyers and sellers have many different ways of measuring value and various reasons (many of them emotional) for buying and selling an asset. Mr. Market is very fickle. The result is an asset may sell at a price significantly below or above its intrinsic or fundamental value.
Intrinsic Value vs. Book Value
The book value of an entity is an accountant’s view of the value of the company. The book value could be the intrinsic value if you believe the accountant’s estimate of assets and liabilities are the true value and there are not intangible values to be considered. But accounting methodology makes it rare that the book value would be a good indication of intrinsic value.
The Relationship with Risk
Risk will affect your investing decisions in two ways. First, the discount rate with which your estimated future cash flows are discounted. This is your required rate of return based on your cost of capital and/or inflation rate.
And second, your required margin of safety will be based on the probable variation of the future intrinsic value of your investment. An investment with large uncertainty requires a greater margin of safety than an investment with less uncertainty.
The Purpose of Intrinsic or Fundamental Value
“Inefficient markets do not necessarily give the participants generous returns. Rather, in my view that they provide the raw materials — mispricings — that can allow some people to win and others to lose on the basis of differential skill.”
Howard Marks
The purpose of estimating intrinsic value is to take advantage of mis-priced assets. If the market value of an asset is below intrinsic value then the investor might consider owning the asset. If the market value of an asset is above intrinsic value then the investor should choose to not own the asset.
The required margin of safety is the amount of discount (below the intrinsic value) an investor desires in order to purchase the asset. A value investor searches for assets with the greatest margin of safety. That means finding assets with a market price far below the investor’s perceived intrinsic value.
Why is Intrinsic Value So Hard to Calculate?
The degree of difficulty in estimating intrinsic value varies greatly among different assets. For example, the intrinsic value of a bond is easier to calculate than its corresponding equity stock. A bond has set cash flow and set duration. Therefore, cash flow and growth are usually fixed. The only variable is the amount the analyst chooses to discount the risks of the bond coupon (interest) not being paid and the cost of capital.
A stock has many more variables, both tangible and intangible, that can affect future cash flow, growth, and the discount for risk. All things being equal, you will require a larger margin of safety for a stock than for a bond.
The tangible assets of intrinsic value are available for analysis because this is the purpose of financial statements. But financial statements can’t reflect the true value of intangible assets such as proprietary technology, trademarks, patents, brands, research and development, good or bad management, competitive advantages, etc. Many times intangibles would be the cause of the greatest disparities between intrinsic values, market values, and book values.
Don’t get discouraged because you feel it’s difficult to determine the intrinsic value of a stock. It is not a science! Any calculations that involve the future are subject to a wide margin of error. There are too many variables and possible end results for anyone to be expected to make precise calculations of intrinsic value.
In fact it is those variables that make up your estimated intrinsic value that are more important than an exact intrinsic value number. So don’t get too fixated on an exact number. The best analysts will have a clear understanding of the variables. It is the variables that determine your required margin of safety.
Interested in Dividends?
“You have to have the knowledge to enable you to make a very general estimate about the value of the underlying business. but you do not cut it close. That is what Ben Graham meant by having a margin of safety. You don’t try to buy businesses worth $83 million for $80 million. You leave yourself an enormous margin. When you build a bridge, you insist it can carry 30,000 pounds, but you only drive 10,000 pound trucks across it. And the same principle works in investing.”
Warren Buffett
The Relationship with Margin of Safety
“The secret to investing is to figure out the value of something – and then pay a lot less.”
Joel Greenblatt
The required margin of safety is the amount of discount (below the intrinsic value) an investor desires in order to purchase the asset. A value investor searches for assets with the greatest margin of safety. That means finding assets with a market price far below the investor’s perceived intrinsic value.
Here is the important concept: After determining a reasonable range for intrinsic value, require a sufficient margin of safety to allow for unforeseen problems and/or your mistakes. In other words, the wider the range of your estimated intrinsic value then the larger your required margin of safety.
High uncertainty in intrinsic value combined with a small margin of safety equals high risk. Low uncertainty combined with a large margin of safety equals low risk.
It’s helpful to approach risk a little differently. Think about searching for investments in which the perceived risk is greater than the real risk. Usually this means the price is lower than the real value. You would want to avoid investments where the perceived risk is less than the real risk. In this case the stock would probably be overpriced.
Ultimately low risk means having a sufficient margin of safety! The best risk/reward ratio investments are found by purchasing assets at prices far below their intrinsic value. In other words, finding mis-priced securities is the best approach to lowering risk and increasing returns.
Price is what you pay. Value is what you get.
Warren Buffett
Additional Reading: My Formula for Analyzing Intrinsic Value
Minimize Large Portfolio Drawdowns
Invest With Confidence in Less Time - Manage Your Portfolio Without Behavioral Errors
