Dividend Value Builder Newsletter
Standard Deviation, Probability, and Risk When Making Investment Decisions
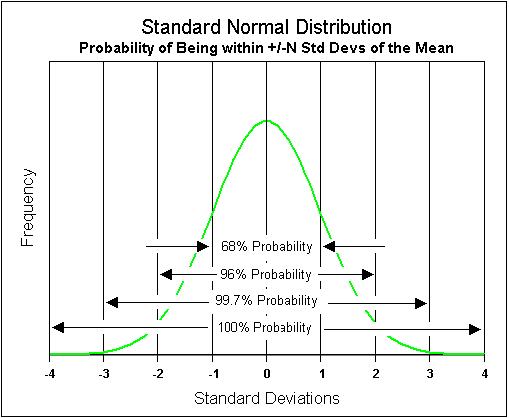
Standard deviation and probability are concepts that make us better risk managers because they cause us to consider lower probability outcomes when making investment decisions.
What is Standard Deviation?
Standard deviation is a historical statistic measuring volatility and the dispersion of a set of data from the mean (average). In other words, the concept of standard deviation is to understand the probability of outcomes that are not the mean.
An investor does not need to know the exact definition or formula to understand the concept of standard deviation.
The purpose of this article is to understand the concept of standard deviation and probability and how they relate to risk and making investment decisions.
We understand we must accept risk to achieve investment returns above the risk-free rate of return. But accepting risk blindly is not sound investing. The mean is almost never the actual return. Standard deviation is a measure of the volatility, or how far away from the mean the outcomes will be based on probability. We need to be cognizant of the negative outcomes that are far away from the mean.
Standard Deviation and Volatility
A small-cap stock will typically have a high standard deviation compared to a stable blue chip dividend stock. The small-cap stock may have a greater amount of uncertainty, volatility, and possible illiquidity. In other words, the probability of the return on the small-cap stock being farther away from the mean is greater than the stable blue chip dividend stock.
The importance and/or size of the item being analyzed determines how critical the outer or smaller probabilities are to the investor. If we consider a 1% position in a volatile stock an investor may choose to accept a large dispersion of possible outcomes. The investor recognizes that regardless of the expected rate of return the volatile stock may have returns from negative 100% to positive 100% or even greater. Because it is only 1% of the portfolio the investor may be willing to accept the large amount of uncertainty.
Retirement Withdrawal Rate Example
Let’s consider a retiree making a decision on how much they want to withdraw from their retirement plan to live on in retirement. Would we not want to be more conservative about such a decision than we would about buying a 1% stock position?
As an example, if we determined that a 5% per year retirement withdrawal rate would give us an 80% chance of not running out of money in our lifetime; would that be a risk we would be willing to take? Most people would probably desire to have the odds higher than that. Therefore they might have to choose a lower withdrawal rate.
In other words, we might be willing to accept a 60% probability of success (profit) when buying a particular stock. At the same time, an 80% probability of success to have enough retirement income might be completely unacceptable.
Making Investment Decisions
These are examples of the importance of understanding the concept of standard deviation and probability. The importance of the decision would have a large influence on how much uncertainty we are willing to accept. A crucial decision such as a retirement withdrawal rate would require greater consideration of lower probability negative outcomes than a decision on a 1% stock position.
The concepts of standard deviation, probability, and risk are crucial financial risk management concepts that allow us to consider lower probability outcomes when making investment decisions.
Portfolio Investment Loss Example
In an AAAMP Value Blog post we look at the importance of an investor determining maximum probable loss as the first step toward developing a risk management plan and a target asset allocation.
This process is an exercise in considering negative outcomes that are far from the mean and their effect on investment returns. The article demonstrates the importance of not losing a large percentage of a portfolio because of the difficulty of getting back to breakeven. Because of the devastation a large loss inflicts on a portfolio, the analysis of the probability of large negative returns is critical to long term investment planning.
The AAAMP Value Blog offers a wide variety of articles on subjects pertaining to wise conservative investing. We only want to take those risks where the odds are heavily in our favor. I can help you make wise decisions through this blog and/or my membership services.
Additional Reading:
5 Portfolio Risk Management Strategies
Minimize Large Portfolio Drawdowns
Invest With Confidence in Less Time - Manage Your Portfolio Without Behavioral Errors
